1. John Napier
(1550 - 1617)
John Napier adalah anak Sir Archibald Napier dari istri pertama, Janet Bothwell, lahir di puri Merchiston, dekat Edinburgh, Skotlandia. Sir Archibald meninggal pada tahun 1608 dan John Napier menggantikannya dan tinggal di puri Merchiston sepanjang hayatnya. Napier meninggal di purinya pada tanggal 3 April 1617, dan dimakamkan di gereja St. Cuthbert, Edinburgh.
penemuan Napier tentang sebenarnya sangat sederhana. Menggunakan progresi geometrik dan integral secara bersamaan. Ambillah sebuah bilangan tertentu yang mendekati angka 1.
Napier menggunakan 1 – 107(atau 0,9999999) sebagai bilangan. Sekarang, istilah progresi dari pangkat yang terus meningkat sampai akhirnya hasilnya mendekati – sangat sedikit selisihnya. Untuk mencapai “keseimbangan” dan menghindari terjadi (bilangan) desimal dikalikan dengan 107. N = 107(1 – 1/107)L, dimana L adalah logaritma Napier sehingga logaritma dari 107 sama dengan nol, yaitu: 107 (1-1/107) = 0,9999999 adalah 1 dan seterusnya. Apabila bilangan tersebut dan logaritma dibagi 107, akan ditemukan - secara virtual – sistem logaritma sebagai basis 1/e, untuk (1-1/107)107 mendekati Lim n→∞ (1 – 1/n)n = 1/e.
Perlu diingat bahwa Napier tidak memunyai konsep logaritma sebagai dasar, seperti yang kita ketahui sekarang. Prinsip-prinsip kerja Napier akan lebih jelas dengan menggunakan konsep geometri di bawah ini.
A P B
C D Q E
Garis AB adalah setengah dari garis CE. Bayangkan titik P berangkat dari titik A, berjalan menyusur garis AB dengan kecepatan semakin menurun dengan proporsi sebanding dengan jaraknya dari titik B; pada saat bersamaan titik Q bergerak pada garis CE dengan kecepatan bergerak sama seperti titik P. Napier menyebut peubah (variabel) jarak CQ adalah logaritma dari jarak PB adalah difinisi geometrik Napier. Misal: PB = x dan CQ = y. Apabila AB dianggap 107, dan jika kecepatan bergeraknya P juga 107, maka dalam notasi kalkulus modern didapat dx/dt = -x dan dy/dt = 107, x0 = 107, y0 = 0. Jadi dy/dx = - 107/x, atau y = -107 ln cx, dimana c adalah inisial kondisi untuk menjadi 10-7. Hasil, y = -107 ln (x/107) atau y/107 = log 1/e(x/107).
2. Wilhelm Schickard
Dia lahir di Herrenbreg 22 April 1592 dan meninggal pada 24 Oktober 1635. ia adalah seorang polymath berkebangsaan jerman. Wilhelm Schickard membuat kalkulator mekanik pertama pada tahun 1623. kalkulator mekanik tersebut dapat bekerja dengan 6 digit. Kepler mendorong Wilhelm Schickard untuk berpikir tentang membuat sebuah mesin untuk mechanise perhitungan astronomi yang ia lakukan. Pada tahun 1619 ia meninggalkan pekerjaannya di Gereja Lutheran ketika dia diangkat sebagai profesor bahasa Ibrani di Universitas Tübingen. Wilhelm Schickard adalah seorang ilmuwan universal dan diajarkan bahasa asli Alkitab seperti Aram serta Ibrani. Salah satu penemuannya untuk membantu murid-muridnya adalah 'Hebraea Rota'. Perangkat mekanik ditampilkan konjugasi kata kerja Ibrani dengan memiliki dua disk berputar diletakkan di atas satu sama lain, masing-masing bentuk konjugasi muncul di jendela.
Selain bahasa Ibrani, dia termasuk astronomi, matematika dan survei. Dalam astronomi ia menemukan sebuah proyeksi kerucut untuk peta bintang di Astroscopium. Bintangnya peta 1623 terdiri dari kerucut dipotong sepanjang meridian titik balik matahari dengan tiang di pusat dan puncak kerucut. Jauh sebelum Pascal dan Leibniz, Schickard menciptakan mesin penghitung, yang 'Rechenuhr', pada tahun 1623. Kepler berminat untuk memiliki salah satu kalkulator Schickard sejak Schickard memberi instruksi untuk satu akan dibangun baginya. Namun, komputer setengah dibangun dihancurkan oleh api. saat ia dijelaskan dalam surat lain untuk Kepler ditulis pada 25 Februari 1624. Dalam surat ini dia memberikan beberapa rincian lebih lanjut dari cara mesin dibangun:
deskripsi yang lebih rinci dari desain mesin aritmatika; dalam ringkasan, ia bekerja sebagai berikut: aaa adalah tombol-tombol pada silinder vertikal dengan angka dari tabel perkalian, yang dapat ditampilkan di akan di jendela disediakan untuk BBB slide. Akan memanggil ddd melekat pada roda bergigi internal, masing-masing memiliki sepuluh gigi diarahkan sedemikian rupa sehingga, jika roda di sebelah kanan membuat sepuluh berubah, roda di kiri hanya membuat satu giliran, dan jika roda pertama di sebelah kanan sisi membuat seratus berubah, roda ketiga di sebelah kirimembuat satu giliran, dan seterusnya. Semua roda berputar pada arah yang sama membuat diperlukan penggunaan lain roda dengan ukuran yang sama diarahkan secara permanen ke roda di sebelah kiri, tetapi tidak dengan satu di kanan, yang memerlukan perhatian khusus selama konstruksi. Angka-angka yang ditandai pada setiap roda ditampilkan di CCC bukaan dari pelat pusat. Akhirnya, eee tombol, yang terletak di atas dasar, yang digunakan untuk menampilkan dalam bukaan fff angka-angka yang perlu digunakan selama operasi.
Kistermann mempelajari desain dari kalkulator Schickard dan menjelaskan "arsitektur" mesin dalam. Schickard menggunakan perkalian ringkasan untuk mesinnya. Sketsa kalkulator telah diawetkan dalam naskah-naskah yang ditinggalkan oleh Schickard dan Kepler. Bruno von Freytag Löringhoff dibangun komputer antara tahun 1957 dan 1960 menggunakan sketsa dan deskripsi dalam surat Schickard. Dia kemudian menguji berbagai perhitungan yang mungkin untuk mencoba untuk memastikan apa tujuan Schickard telah dalam membangun mesin penghitung. Von Freytag Löringhoff menemukan bahwa itu bekerja dengan baik dan sangat cocok untuk melakukan perhitungan astronomi yang diperlukan untuk astronom abad ketujuh belas.
3. Blaise Pascal (1623-1662)
Blaise Pascal adalah seorang ahli matematika, fisikawan, penemu, penulis dan filsuf Kristen berkebangsaan Perancis. Ia lahir di Clermont-Ferrand, Perancis pada 19 Juni 1623 dan meninggal di Paris, Perancis pada 19 Agustus 1662 pada umur 39 tahun. Bersama dengan Pierre de Fermat menemukan teori tentang probabilitas. Pada awalnya minat riset dari Pascal lebih banyak pada bidang ilmu pengetahuan dan ilmu terapan, di mana dia telah berhasil menciptakan mesin penghitung yang dikenal pertama kali. kalkulator mekanik ini berkapasitas 8 digit. Mesin itu hanya dapat menghitung (mesin komputasi sederhana yang merupakan cikal bakal kalkulator). Alat hitung ini menggunakan roda penghitung yang digunakan untuk menjumlah bilangan. Alat hitung ciptaan Pascal mampu mengoperasikan penambahan, pengurangan dan pembagian dua bilangan sekaligus. Pascal mengutamakan metode re-zeroing untuk mesin hitung temuannya ini. Sehingga ia dapat membuktikan bila mesin hitung ciptaannya tersebut dapat dioperasikan dan dapat berfungsi semuanya, sehingga membuktikan bila mesin hitung ini benar-benar berkualitas. Selain itu, Pascal juga menemukan prinsip kerja barometer, sistem kerja jam tangan, rumus segitiga pascal, rumus geometri.
Riwayat Hidup Blaise Pascal
Di usia 12 tahun, ia sudah bisa menciptakan sebuah mesin penghitung untuk membantu pekerjaan ayahnya Étienne Pascal. Ayahnya adalah seorang petugas penarik pajak yang bekerja di wilayah Auvergne, Perancis. Karya-karyanya terus bertambah mulai dari merancang bangunan segienam (hexagram), menemukan prinsip kerja barometer, sistem kerja arloji, hingga ikut terlibat dalam pembuatan sistem transportasi bawah tanah kota Paris. Pada tahun 1642, saat masih remaja ia mulai membuat percobaan pada mesin hitung. Setelah selama tiga tahun berusaha dan menghasilkan lima puluh prototipe, ia menemukan kalkulator mekanik. Kemudian dalam sepuluh tahun berikutnya Ia membangun 20 mesin ini (disebut kalkulator Pascal dan kemudian Pascalines). Mesin ini bisa menambah dan mengurangi dua nomor secara langsung dan berkembang biak dan membagi dengan pengulangan. Pascal mengutamakan metode re-zeroing untuk mesinnya. Dengan demikian ia membuktikan sebelum dioperasikan kalkulatornya berfungsi penuh. Pascal menulis sebuah risalah yang signifikan pada subyek geometri proyektif pada usia 16, dan kemudian berhubungan dengan Pierre de Fermat pada teori probabilitas, sangat mempengaruhi perkembangan ekonomi modern dan ilmu sosial.
4. Gottfried
Wilhem Leibniz (1646-1716)
Leibniz lahir di kota Leipzig, sachsen pada tahun 1646. Leibniz meninggal pada tahun 1716 dengan usia 70 tahun di Hanover, Saxony. Ia adalah seorang filsuf Jerman keturunan Sorbia dan berasal dari Sachsen. Selain seorang filsuf, ia adalah ilmuwan, matematikawan, diplomat, fisikawan, sejarahwan dan doktor dalam hukum duniawi dan hukum gereja. Pada usia 12 tahun ia telah mengembangkan beberapa hipotesa logika yang menjadi bahasa simbol matematika. Kebanyakan ahli sejarah percaya bahwa Newton dan Leibniz mengembangkan kalkulus secara terpisah. Keduanya pula menggunakan notasi matematika yang berbeda pula. Menurut teman-teman dekat Newton, Newton telah menyelesaikan karyanya bertahun-tahun sebelum Leibniz, namun tidak mempublikasikannya sampai dengan tahun 1693. Ia pula baru menjelaskannya secara penuh pada tahun 1704, manakala pada tahun 1684, Leibniz sudah mulai mempublikasikan penjelasan penuh atas karyanya. Notasi dan "metode diferensial" Leibniz secara universal diadopsi di Daratan Eropa, sedangkan Kerajaan Britania baru mengadopsinya setelah tahun 1820. Dalam buku catatan Leibniz, dapat ditemukan adanya gagasan-gagasan sistematis yang memperlihatkan bagaimana Leibniz mengembangkan kalkulusnya dari awal sampai akhir, manakala pada catatan Newton hanya dapat ditemukan hasil akhirnya saja. Newton mengklaim bahwa ia enggan mempublikasi kalkulusnya karena takut ditertawakan.
Dalam suatu kesempatan, dalam kunjungan ke London ini, Leibniz menghadiri pertemuan dengan Royal Society, dimana dia menunjukkan cara kerja mesin hitung penemuannya. Penemuan dan hasil karyanya itu membuat Leibniz diangkat sebagai anggota Royal Society berwarganagara asing (bukan orang Inggris) sebelum dia pulang ke Paris pada tahun 1673. Tidak lama kemudian, Leibniz dan Newton pada saat hampir bersamaan diangkat menjadi anggota Akademi Sains Perancis berwarganegaraan asing. Merasa puas dengan prestasi yang diraih Leibniz, Huygens menyuruh anak didiknya ini terus menekuni matematika. Dalam perpisahan dengan Huygens di Paris, guna kembali ke Hanover, Leibniz berjanji akan menggunakan waktu senggangnya untuk menekuni matematika. Tahun 1676, Leibniz mengabdikan dirinya pada Duke Brunswick-Luneburg.
Kalkulus
Newton tidak menyukai perubahan yang sangat kecil (infinitesimal) menuju ke tidak terhingga karena dianggapnya hanya “remah-remah.” Notasi os – dari Newton, pada persamaan-persamaan tentang perubahan (fluxion), karena sekali waktu os beroperasi seperti halnya bilangan nol dan terkadang seperti bukan bilangan nol. Perbedaan yang sangat kecil, lebih kecil dari bilangan positif yang dapat Anda beri nama namun tetap lebih besar dari nol. Bagi matematikawan jaman itu, hal tersebut adalah konsep yang sangat aneh. Newton malu dengan persamaan-persamaan tersebut sehingga hal ini tetap disembunyikan rapat-rapat. Ternyata os yang terdapat pada perhitungan itu hanyalah ‘batu loncatan’ menuju penyelesaian suatu perhitungan.
Sebaliknya, Leibniz memperhatikan perubahan kecil ini, dan tetap terpakai dalam semua perhitungannya; akhirnya derivatif y terhadap x bukanlah merupakan nisbah bebas bilangan maha kecil ini dari perubahan (fluxion) yº/xº, tapi nisbah bilangan maha kecil dy/dx. Kalkulus Leibniz, dengan dy dan dx dapat dimanipulasi seperti layaknya angka biasa. Alasan ini kiranya dapat menjawab pertanyaan mengapa para matematikawan lebih suka menggunakan notasi kalkulus versi Leibniz daripada notasi kalkulus versi Newton. Pada diferensial Leibniz ada “larangan” apabila terjadi 0/0, hal ini harus dihindari, dimana hal ini tidak terdapat pada fluxion Newton. Tahun 1673, Leibniz menyempurnakan notasi-notasi kalkulus versinya dan pada tahun 1675, dia menulis manuskrip dengan menggunakan notasi: ∫f(x)dx untuk pertama kalinya. Tahun 1676, menemukan notasi: d(xⁿ) = nxⁿ‾¹ dx untuk integral dan pangkat n.
Mesin penghitung Leibniz
Tahun 1667, Leibniz tinggal di Frankfurt, bekerja pada Boineburg yang menjabat sebagai sekretaris masyarakat alkimia Nurenburg. Di sini, selama bertahun-tahun, Leibniz terlibat dengan berbagai proyek yang terkait dengan sains maupun politik. Leibniz memulai membuat mesin penghitung, dimana pada tahun 1673 ditemani keponakan Boineburg, dihadapan Royal Society (Inggris), guna mendemontrasikan mesin penghitung yang belum selesai. Mesin penghitung versi Leibniz merupakan penyempurnaan dari mesin penghitung ciptaan Pascal. Blaise Pascal menemukan mesin penjumlah pada tahun 1642 dan pada tahun 1673, Leibniz menemukan mesin yang dapat melakukan operasi perkalian dan pembagian.
Joseph -Marie Jacquard menemukan alat perkakas tenun otomatis yang di kontrol oleh punch card. Joseph Marie Jacquard adalah seorang pembuat topi jerami sebelum menjadi seorang pemintal sutera dan penemu Perancis, yang memperbaiki rancangan awal kartu berlubang dari perkakas tenun jaques de vaucanson tahun 1745, untuk menemukan mekanisme perkakas tenun jacquard antara tahun 1804 - 1805. Mekanisme perkakas tenun Jacquard dikendalikan dengan pola lubang tercatat di seuntai kartu, dan memungkinkan pemintalan pola yang lebih rumit untuk masa kini. Jacquard meninggal di oullins, 17 Agustus 1834.
Josep Marie Jacquard mewarisi usaha pertenunan kecil dari ayahnya yang sudah meninggal dunia. Di tahun 1793, untuk sementara Marie Jacquard meninggalkan usahanya itu dan ikut berperang dalam Revolusi Perancis sebagai seorang Royal Soldier, tentara pendukung kerajaan. Setelah itu dia kembali meneruskan usaha dan cita-citanya untuk membuat mekanisasi dan otomatisasi dalam pembuatan kain tenun. Di tahun 1801, akhirnya dia berhasil mengembangkan otomatisasi pada teknik pembuatan kain tenun ini. Idenya adalah dengan membuat kartu-kartu berlubang (punch card) yang dipasang di atas alat tenun dan dihubungkan sedemikian rupa, sehingga kartu berlubang ini dapat mengontrol kerja masing-masing benang lusi secara bebas. Prinsipnya sederhana namun terbukti sangat efektif. Bagian kartu yang berlubang, melalui suatu mekanisme tertentu, akan menghasilkan gerakan mengangkat benang lusi yang terhubung dengan lubang tersebut. Sebaliknya, bagian tak-berlubang adalah kode perintah mekanik untuk tidak mengangkat benang lusi. Di dalam teknik pembuatan kain tenun terutama yang bermotif gambar, teknik pengaturan benang lusi ini, yaitu kapan ia harus naik dan kapan pula ia harus turun, menjadi titik sentralnya. Semakin kompleks motif kain yang ingin dibuat semakin kompleks pula urutan pengaturan naik-turun helaian benang-benang lusi tersebut, yang jumlahnya bisa mencapai ribuan.
6. Charles Babbage (1791-1871)
Charles Babbage yang lahir 26 Desember 1792, daerah yang sekarang dikenal dengan nama Southwark, London, anak dari Benjamin Babbage, seorang Banker, dan meninggal 18 Oktober 1871 pada umur 79 tahun. Kelebihannya dalam matematika sangat menonjol. Saat memasuki Trinity College di Cambridge tahun 1811, dia mendapati bahwa kemampuan matematikanya jauh lebih baik, bahkan dari pada tutornya sendiri. Di usia 20 tahunan Babbage bekerja sebagai seorang ahli matematika terutama dibidang fungsi kalkulus. Tahun 1816, dia terpilih sebagai anggota "Royal Society" (organisasi sains dan akademis independen Inggris Raya, masih aktif hingga kini) dan memainkan peran penting di yayasan "Astronomical Society" (organisasi Astronomi dan geofisika Inggris raya, masih aktif hingga kini) pada tahun 1820. Pada masa ini Babbage mulai tertarik pada mesin hitung, yang berlanjut hingga akhir hayatnya.
Pada masa itu, perhitungan dengan menggunakan tabel matematika sering mengalami kesalahan. Babbage ingin mengembangkan cara melakukan perhitungan secara mekanik, sehingga dapat mengurangi kesalahan perhitungan yang sering dilakukan oleh manusia. Saat itu, Babbage mendapat inspirasi dari perkembangan mesin hitung yang dikerjakan oleh Wilhelm Schickard, Blaise Pascal, danGottfried Leibniz. Gagasan awal tentang mesin Babbage ditulis dalam bentuk surat yang ditulisnya kepada Masyarakat Astronomi Kerajaan berjudul "Note on the application of machinery to the computation of astronomical and mathematical tables" ("catatan mengenai penerapan mesin bagi penghitungan tabel astronomis dan matematis") tertanggal 14 Juni 1822. Tahun 1821 Babbage menciptakan Difference Engine, sebuah mesin yang dapat menyusun Tabel Matematika. Saat melengkapi mesin tersebut di tahun 1832, Babbage mendapatkan ide tentang mesin yang lebih baik, yang akan mampu menyelesaikan tidak hanya satu jenis namun berbagai jenis operasi aritmatika. Mesin ini dinamakan Analytical Engine (1856), yang dimaksudkan sebagai mesin pemanipulasi simbol umum, serta mempunyai beberapa karakteristik dari komputer modern. Diantaranya adalah penggunaan punched card, sebuah unit memori untuk memasukkan angka, dan berbagai elemen dasar komputer lainnya.
Tahun 1937, tulisan Babbage menjadi perhatian Howard H. Aiken, sarjana tamatan Harvard. Aiken yang juga sedang mencoba menyelesaikan rancangan mesin komputer, tergerak oleh gagasan Babbage. Bekerjasama dengan IBM, Aiken sanggup membuat Mark I, komputer pertama untuk segala keperluan. Dua tahun sesudah Mark I dioperasikan (1946), kelompok insinyur dan penemu lain menyelesaikan ENIAC, mesin hitung elektronik pertama. Sejak itu, kemajuan teknologi komputer berkembang pesat.
7. William Stanley Jevons (1835-1882)
William Stanley Jevons lahir pada tanggal 1 September 1835 di Lierpool, UK.William Stanley JEvons merupakan ahli ekonomi dan pemikir asal Inggris. Bukunya yang berjudul 'The Theory of Political Economy' (1871) merupakan awal dari metode matematik dalam ekonomi. Buku tersebut memuat kasus bahwa ekonomi sebagai ilmu pengetahuan yang berfokus pada kuantitas itu memerlukan matematika. Hasil-hasil pemikiran Jevons disebut-sebut menandai periode baru di sejarah pemikiran ekonomi. Kontribusi Jevons pada revolusi ekonomi di akhir abad 19 menghasilkan reputasi yang baik baginya sebagai politisi ekonomi dan pemikir ulung pada saat itu.
Ibunya, Mary Anne Jevons, merupakan anak dari Willian Roscoe. Pada usia 15 tahun, ia sekolah di University Colleger London. Pada masa ini ia yakin bahwa ia bisa menjadi seorang pemikir yang handal. Setelah dua tahun di Universitas ini, secara tidak diduga ia mendapatkan tawaran untuk menjadi penguji nilai logam di Australia. Ia akhirnya meninggalkan UK ke Sydney pada Juni 1854 dan berada di sana selama lima tahun. Setelah itu, ia kembali mengenyam pendidikan sambil terus menulis paper tentang ilmu pengetahuan. Tulisan-tulisan tersebut akhirnya menghasilkan sebuah buku berjudul "The Principles of Science'. Beberapa tawaran pun berdatangan sehingga pada 1866, Jevons terpilih sebagai seorang profesor bidang logika dan mental dan filosofi moral. Setahun kemudian, Jevons menikahi Harriet Ann Taylor. Jevons banyak berkontribusi pada ekonomi dan logika, termasuk melalui papernya 'A General Mathematical Theory of political Economy' yang ditulis pada 1862. Tidak sampai setahun dari penerbitan paper tersebut, Jevons mengenal aplikasi matematika ke politik ekonomi yang dibuat oleh penulis terdahulu.
8. Herman Hollerith (1860-1929)
Herman Hollerith lahir tanggal 29 Februari 1860 dan meninggalkan dunia pada 17 November 1929. Dia seorang ahli statistik Amerika Syarikat yang mengembangkan penjadwal mekanik berdasarkan kadbuk supaya dapat menjadwalkan statistik dengan cepat daripada jutaan data.Dia adalah keturunan Jerman dan Amerika. Peranan dalam sejarah komputer adalah dialah yang membangun mesin tabulator berbasiskan punched cards. Dengan fungsi untuk mempercepat pemrosesan statistik yang terdiri dari jutaan data. Hollerith mengembangkan cara untuk membuat pemicu sebuah koneksi eletrik untuk alat perhitungan dan penyimpan informasi. Cara ini berasal dari ide bahwa data dapat di kodekan dengan angka. Dia melihat bahwa data dapat diletakkan (lubang) pada lokasi yang spesifik pada sebuah kartu (punched card). Kemudian kartu tersebut dapat dihitung atau diurutkan dengan mesin. Dan juga data dapat disimpan. Ini adalah ide dasar dari komputer zaman sekarang.
Sebuah perjalanan panjang dari sejarah komputer. Berawal dari sempoa, pascaline kemudian Charles babbage Berikut beberapa data perkembangan karirnya yang saya translate dari sebagian artikel berbahasa inggris. Hollerith mulai bekerja untuk Kantor Sensus Amerika Serikat pada tahun pertama ia membangun aplikasi paten. Berjudul "Art of Compiling Statistik", ia mendapatkannya pada 23 September 1884, US Paten No 395782 diberikan pada 8 Januari 1889. Mesin Hollerith yang dibangun di bawah kontrak untuk Kantor Sensus, yang digunakan mereka hanya dalam satu tahun. padahal sensus 1880 yang telah diambil delapan tahun.
Hollerith kemudian memulai usaha sendiri di 1896, mendirikan Tabulating Machine Company. Sebagian besar utama biro sensus di seluruh dunia membeli peralatan dan kartu itu, sebagai perusahaan asuransi yang besar. Untuk membuat sistem kerja nya, dia jadiakn pertama otomatis kartu-pakan mekanisme dan pertama kunci punch (yakni suatu punch yang dioperasikan dari keyboard), yang diperbolehkan yang terampil ke operator kartu punch 200-300 per jam. Dia juga yang membuat tabulator. Hardwired tabulator 1890 yang telah beroperasi pada 1890 hanya Sensus kartu. Sebuah panel kontrol di 1906 Tipe I tabulator diizinkan untuk melakukan pekerjaan yang berbeda tanpa harus dibangun ulang (langkah pertama menuju program). Penemuan ini merupakan dasar dari informasi yang modern industri.
9. Alan Mattison Turing (1912-1954)
Alan Mattison Turing lahir di Paddington London, 23 Juni 1912. Dalam penelitiannya Turing lebih banyak "menciptakan kembali" dibandingkan "menggunakan" temuan yang sudah ada. Setelah lulus Turing mendapat keanggotaan di King's College (1935). Pada saat ini lah Turing mempunyai konsep mengenai "Mesin Turing". Melalui sebuah kuliah, di tahun 1935, Turing diperkenalkan pada pertanyaan berkaitan dengan Logika Matematika, yang di ajukan oleh Hilbert. Ini adalah pertanyaan tentang "Decidability", "the Entscheidungs problem". Menanggapi pertanyaan tersebut Turing memberikan solusi mekanikal berupa konsep "Mesin Universal Turing". Dalam konsep ini turing menggambarkan sebuah mesin yang mampu membaca rangkaian beberapa "nol dan satu" (binary digit) yang akan menjelaskan cara penyelesaian masalah matematika, dan menyediakan jawaban yang dibutuhkan. Inti dari mesin ini yang dikemudian hari dikenal sebagai ide tentang sebuah komputer. Mesin ini masih berupa konsep, sampai kemudian diwujudkan dalam bentuk nyata beberapa tahun kemudian.
Selama perang dunia II(1939-1945), Turing bekerja pada Depertemen Komunikasi Britania Raya. Disana dia ditugaskan untuk memecahkan kode sandi yang diciptakan oleh Mesin Enigma milik pihak Jerman. Ini adalah pekerjaan berat karena mesin ini mampu menghasilkan kode yang berubah secara konstan, dan untuk memecahkannya adalah suatu hal yang mustahil pada zaman itu. Namun ternyata itu tidak mustahil bagi Turing, yang kemudian menciptakan "COLOSSUS", sebuah mesin yang mampu memecahkan kode enigma dalam waktu singkat. Mesin ini juga merupakan suatu awal menuju Komputer Digital. Turing juga mempunyai minat yang sangat besar dalam pengembangan "Artificial Intelligence". Untuk itu dia menghabiskan satu tahun di Cambridge untuk mempelajari Neurologi dan Fisiologi. Di tahun 1947 dia menulis sebuah paper (tidak pernah diterbitkan selama hidupnya) mengenai konsep yang sekarang dikenal dengan "jaringan neural", dimana serangkaian sistem kompleks mampu memeliki kemampuan belajar. Kemudian tahun 1950 mengeluarkan paper yang berpengaruh besar berjudul "Computing Machinery and Intelligence". Dalam papernya ini Turing mengusulkan "Tes Turing" sebagai sebuah metode untuk menentukan apakah sebuah mesin memiliku "Artificial Intelligence". Hingga tahun 1990-an Tes ini masih dianggap sebagai cara yang paling baik untuk menentukan intelegensia dari sebuah mesin.
.jpg)


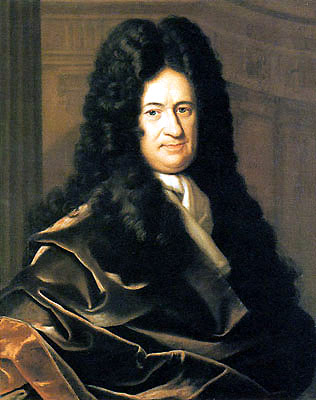






0 komentar:
Posting Komentar